みなさまお疲れ様でした。
成績及び評価はこちらです。
まだ課題をされていない方は早めにやってください。

諸般の事情で遅れるなどトラブルが生じそうな方は、ここの（左側のコメント欄)
掲示板にその旨、記して、お知らせください。

承前

参考までに、参考にしてください

△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼
課題を終了された方は、コメント欄に
名前：学籍番号
メール：空欄
URL：書き込んだブログのURL
コメント：書き込んだ日の日付
　　　　　学籍番号
　　　　　書き込んだ記事のURL
　　　　　課題終了しました

※最後に課題終了した旨、書き込んでください。
受け付けた場合はここにリンクした上で、評価を書き入れておきます。
△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼

サンプルデータをUPしておきます。
データが探せなかったり，うまく作れないという場合に利用してください。

【edu.dat】
47都道府県の教育関連の16変数のクロスセクションデータ
出所：社会生活統計指標　－都道府県の指標－2007

【econ.dat】
47都道府県の県内生産と総支出，1人当たり所得の３変数のクロスセクションデータ
出所：経済成長率及び１人当たり県民所得

このデータによる回帰分析，主成分分析，クラスター分析の出力例は前回、PowerPoint用に作成しておいたファイルを解凍したしたもののなかのテキストファイルにあります。参考にしてください。
内容は，これまでのおさらいですが，分からないところは質問するなり私に聞いてください。

PowerPointで作成する方が楽だと判断された場合は以下のメールアドレスへ添付ファイルとして送信してください。

okh.2007@gmail.com


前回、解凍ファイルにあったテキストファイルに記述されていたRのcodeのコメント付きファイルです。

サンプルのデータ『edu.dat』と『econ.dat』をマージして
『regn』というデータセットを生成しています。
このデータを例示した目的は
都道府県別教育及び進学率関連データと
都道府県の経済力を示すGDP、GDE成長率と1人あたり所得
との関係を見るためのものです。

進学率が高いと所得が高いとか、
長欠児童が多いと経済成長が鈍るとか、
様々な仮説が考えられます。
データを多角的に眺めて、各自で分析or解析してみてください。
もちろんR以外のソフト、電卓やExcelで作業してもかまいません。

目的はあくまでも、図と文字の情報をブログなどで表示し、
情報発信することなので分析の中身は問いません。
自由にデータ解析してください。
ブログなり、PPTなりの見た目がきれいなものであることが望ましいです。

終了した方は掲示板にそのもく、明記してください。成績評価リストに結果を表示します。

前回の説明どおりです。

ただし、ほんのさわりですがPowerPointの使用法を説明します。

PPTの作業用部品
図形ファイル：３
テキストファイル：１

圧縮ｌｚｈ
text.lzh

保存場所
sample_data
edu.dat
econ.dat
サンプルデータをUPしておきます。
データが探せなかったり，うまく作れないという場合に利用してください。
【edu.dat】
47都道府県の教育関連の16変数のクロスセクションデータ
出所：社会生活統計指標　－都道府県の指標－2007
【econ.dat】
47都道府県の県内生産と総支出，1人当たり所得の３変数のクロスセクションデータ
出所：経済成長率及び１人当たり県民所得
このデータによる回帰分析，主成分分析，クラスター分析の出力例は解凍されたファイルのテキストファイルにあります。参考にしてください。
内容は，これまでのおさらいですが，分からないところは質問するなり私に聞いてください。

PowerPointで作成する場合は以下のメールアドレスへ添付ファイルとして送信してください。

okh.2007@gmail.com

ドキュメンテーションです。
プレゼンテーションでもいいです。
とりあえず，どっちでもいいです。

とりあえず与えられたテーマに沿って，何かコンテンツ（というほどのものでもないかもしれないが）を作って公開してもらいます。
これまでにやった解析手法を大いに活用してもらいたい。

１．テーマ設定
２．資料収集
３．データ作成
４．データ解析
５．結果の解釈
６．結果を『他人に理解してもらえるような形で記述』
７．公開

因みにWORD，Excelで作成したものは，そのままHTML形式で保存して，Web表示できます。
でかいです。
とてつもなくでかいですし，迷惑なことに，図形などは新たにディレクトリを作成してくれたりします。
ということはPowerPoint（以下PPT）でも同様です。

今回は，BlogとPPTを使ってコンテンツ（というほどのものでもないかもしれないが）を完成させます。
ところでこの教室はOffice2007ですが，私は持っていませんし，いまひとつ気が進みません。現在2003からOpenOffice.orgに移行中なのでどうしたものかと。
そこらへんは考えておきます。

△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼
とりあえず，習うより慣れろで，参考に一つ作ってみます。まねしてください
頭ではなく，手で理解してください。
「分かる」 ≠ 「できる」です。
△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼△▼
１．昨年の選挙で仲井間知事は失業率云々を公約にあげたが，失業率を考える。
２．とりあえず沖縄と全国の失業率を比べてみる。まずは沖縄県統計課へ。
３．失業率のデータを作ろう。ExcelをRで読み込めるように整形しよう。
４．時系列データなので時系列分析で将来予測をやってみるか。
５．なるほど，おお，未来が見えた？
６．とりあえずドキュメント作成。
７．公開

☐◆☐◆☐◆☐◆☐◆☐◆☐◆☐◆☐◆
ここから実際の作業をシミュレートしましょう
☐◆☐◆☐◆☐◆☐◆☐◆☐◆☐◆☐◆

沖縄県統計課に行く

　　　　　　　　　　　　　　　　　　　　　　　　　　どうも，これっぽい。
全国のデータは

　　　　　　　　　　　　　　　　　　　　　　　　　　どうも，それっぽい。
ここから「総務省」→「労働力調査」→「統計表一覧」→「長期時系列データ」をたどっていく。

両方のサイトからExcelのファイルを引っ張ってきて，整形する。

こういうときExcelはは不便だ。ASCII保存してAWKとかで編集できると楽。

メモ帳などのテキストエディタにExcelのデータを貼り付ける。
（もちろん，CSVで保存したり，直接読み見込むことも可能，例えば
こっちとあっち
特にあっちは秀逸

・*:.。..。.:*・∽・*:.。..。.:*・∽・*:.。..。.:*・∽・*:.。..。.:*・・*:.。..。.:*・∽・*
参考：　整形したExcel File 　　⇒　　からコピペしたテキストファイル
あくまで参考なので，自分で作業したほうが後々のため良い。
ただしExcel使いにだけはなりたくない，という志の高い方は
私が作ったやつをそのまま使ってください。
・*:.。..。.:*・∽・*:.。..。.:*・∽・*:.。..。.:*・∽・*:.。..。.:*・・*:.。..。.:*・∽・*
undat<-read.table("c:/00dat/unemp.txt",T)
plot(undat)
ts.plot(undat)


ts.plot(undat,gpars=list(xlab="年",ylab="失業率"),lty=c(1:2),col=c(1:2))
legend(locator(1),c("沖縄","全国"),lty=c(1:2),col=c(1:2))
##　凡例を置きたい場所をクリックする

多変量時系列分析をする訳ではないので，データ系列を分割しよう。
時系列オブジェクトに変換する前に
attchで扱ってもいいと思うが，とりあえず
変数名が日本語なので分割して英字にしよう。

attach(undat)
okn<-沖縄
jpn<-全国

okn<-ts(okn,start=c(1996,1),frequency=12)
jpn<-ts(jpn,start=c(1996,1),frequency=12)

## 勿論こっちでも良い。
## okn<-ts(undat$沖縄,start=c(1996,1),frequency=12)
## jpn<-ts(undat$全国,start=c(1996,1),frequency=12)

plot(okn)

横軸のラベルが多少良くなった。

時系列分析いきます。

（1） 自己相関，相互相関
par(mfrow=c(3,1))
acf(okn)
acf(jpn)
ccf(okn,jpn)

（2） 偏自己相関
par(mfrow=c(2,1))
pacf(okn)
pacf(jpn)

（3） ピリオドグラムとその平滑化
par(mfrow=c(2,2))
spec.pgram(okn)
spec.pgram(okn,spans=c(3,3))
spec.pgram(jpn)
spec.pgram(jpn,spans=c(3,3))

（4） スペクトル
par(mfrow=c(1,2))
spectrum(okn,method="ar")
spectrum(jpn,method="ar")

(3)はいらないと思うけど,(4)よりデータには
トレンドがあり非定常である。
なんのこっちゃ，
と思うかもしれませんが，スペクトルは周波数という視点から，データを眺めたもので，横軸は【１／ｆ】で周波数分の逆数＝周期を意味します。
ので，このデータには長周期あるいはトレンドが見出せるわけです。

スペクトルの見方は面倒なので，Web上にあげませんから。実習室でしっかり聞いといてください。
トレンド，周期成分，ホワイトノイズの３つを図示説明します。

（＿）/　とりあえず頭を空にして以下のコードを走らせてみよう
## １回差分をとってみる
par(mfrow=c(2,1))
acf(diff(okn))
acf(diff(jpn))

par(mfrow=c(2,1))
pacf(diff(okn))
pacf(diff(jpn))

par(mfrow=c(1,2))
spectrum(diff(okn),method="ar")
spectrum(diff(jpn),method="ar")

## ARIMA(1,1,1)にしてみる
par(mfrow=c(1,1))
(okar<-arima(okn,order=c(1,1,1)))
ts.plot(okar$residuals)
(okpr<-predict(okar,n.ahead=24))
okup<-okpr$pred+1.96*okpr$se
okdn<-okpr$pred-1.96*okpr$se
ts.plot(okn,okpr$pred,okup,okdn)

(jpar<-arima(jpn,order=c(1,1,1)))
ts.plot(jpar$residuals)
(jppr<-predict(jpar,n.ahead=24))
jpup<-jppr$pred+1.96*jppr$se
jpdn<-jppr$pred-1.96*jppr$se
ts.plot(jpn,jppr$pred,jpup,jpdn)

par(mfrow=c(2,1))
ts.plot(okn,okpr$pred,okup,okdn,gpars=list(lt=c(1,2,3,4),col=c(1,2,3,4)))
ts.plot(jpn,jppr$pred,jpup,jpdn,gpars=list(lt=c(1,2,3,4),col=c(1,2,3,4)))

##　安易な予測を反省してみる
##　ARIMA(10,1,2)！！で盲省する
(okar<-arima(okn,order=c(10,1,2)))
(okpr<-predict(okar,n.ahead=24))
okup<-okpr$pred+1.96*okpr$se
okdn<-okpr$pred-1.96*okpr$se

##　ARIMA(10,1,10)！！で脱力する
(jpar<-arima(jpn,order=c(10,1,10)))
(jppr<-predict(jpar,n.ahead=24))
jpup<-jppr$pred+1.96*jppr$se
jpdn<-jppr$pred-1.96*jppr$se

par(mfrow=c(2,1))
ts.plot(okn,okpr$pred,okup,okdn,gpars=list(lt=c(1,2,3,4),col=c(1,2,3,4)))
ts.plot(jpn,jppr$pred,jpup,jpdn,gpars=list(lt=c(1,2,3,4),col=c(1,2,3,4)))


SAMPLEのBlogはここ，PPTはここにあります。

本日はとりあえずここまでとし，続きは次回とします。

皆さんは，統計データのサイトやらをブラウジングして
扱ってみたいデータとかを探しておいてください。

確か、ここで議論した覚えがある。

Rの表示部（コンソール）の日本語化、あるいは取り扱う変数の多言語化（内部的なメモリー領域の拡張）は設定ファイルで行っている。R2.x.x時の議論だが今でも変わらんでしょう。最新版では設定ファイルの自動書き換えのモジュールがあるというが、確認はしてないです。

例えば、通常の環境ではCドライブのProgram FilesディレクトリにあるRの各バージョンのフォルダ内の『etc』というディレクトリ（2.4.1では下のようになります。）内の設定ファイルを書き換えればよい。



この例では念のために、オリジナルファイルのバックアップを取っています。
拡張子BAKのやつがそれ。

C:\Program Files\R\R-2.4.1\etc内の『Rconsole 』と『Rdevga』の中身を書き換えるというもの。
因みに、Win系と違ってU/Linux系ではこのような設定ファイルで環境を設定するのが主流。
というよか何かと便利。
有名なのは.htaccesといったファイル名の先頭が「．」で始まるドットファイル。
俗称インターネットをやっていると良く出くわすんじゃなかろうか。


なお、これは過去に多々あったことだが、新規バージョンを使うと、旧バージョンで使えたライブラリが使用できないことがあり（特に、特定分野での最新の解析法とされるモジュールに多い）、要注意。
やはり、致命的バグでないかぎり安定バージョンを使用するのが無難。

GNU的なFSFの最新版というやつは大体ディベロッパー向けだったりするからね。

追記：問題はWin標準付属のエディタであるメモ帳（notepad.exe）で保存すると改行コードが変換されなかったというものだったと思う（うろ）。
そのときはwordpadでもいいけど，ｘｙｚｚｙをお勧めする。

因みにR-2.5.0はfontを”MS Gothic”に変えるだけでうまくいったけど。

データの読み込み
dat01<-read.table("n:/6-18.txt",T)
距離行列の定義
dd<-dist(dat01)
各メソッドでのクラスター形成
ddhc1<-hclust(dd)
ddhc1<-hclust(dd,"single")
ddhc2<-hclust(dd,"complete")
ddhc3<-hclust(dd,"average")
ddhc4<-hclust(dd,"centroid")
ddhc5<-hclust(dd,"median")
ddhc6<-hclust(dd,"ward")
描画その１
plot(ddhc1,main="最近隣法")
plot(ddhc2,main="最遠隣法")
plot(ddhc3,main="群平均法")
plot(ddhc4,main="重心法")
plot(ddhc5,main="メディアン法")
plot(ddhc6,main="ウォード法")
描画その２
plot(ddhc1,hang=-1,main="最近隣法")
plot(ddhc2,hang=-1,main="最遠隣法")
plot(ddhc3,hang=-1,main="群平均法")
plot(ddhc4,hang=-1,main="重心法")
plot(ddhc5,hang=-1,main="メディアン法")
plot(ddhc6,hang=-1,main="ウォード法")

情報量の縮約と多変量データの解析手続き

今回までに以下の２つの技法を身につけたことになるが？
どうでしょう。

１．重回帰
２．主成分分析
３．クラスター分析

どうも自信がないという方は、前回までのドキュメントと関連するリンクに一通り目を通してみてください
微かに分かり、分った積もり、程度で十分です。詳細は統計や計量経済関連の講義等でカバーできると思います。
また、RjpWikiにも膨大な資料がストックされていますので、参照してください。

今回はクラスター分析の説明をします。

クラスターというのは産業政策の分野では流行っているようですが。聞いたことあるでしょうか。
いわゆる産業クラスターというやつです。興味のある方、経済産業省のホームページを参照してください。沖縄では「OKINAWA型産業振興プロジェクト」として沖縄総合事務局経済産業部で担当しています。
またエアコンなどの家電製品でも分子クラスターとか最近よく聞きます。

産業クラスターではクラスターのことを「ブドウの房」と説明していますが、クラスター分析で言う「クラスター」とは
生物や企業などのデータを似たもの同士にグループ分けしたりする分類のための数理的手法
といったようなものです。


クラスター分析は別名数値分類法（numerical taxonomy）ともいう。

クラスター分析の利用法をBall(Classification Analysis:1971)は7つあげている。

1. 真の類型を見出す
2. モデルの当てはめ
3. グループ化に基づく予測
4. 仮設の検定
5. データ探索
6. 仮設形成
7. データ集約

クラスター分析は類似の度合いを定量化するが、その測定法は類似度と非類似度に大別される距離の計測による。

距離
1. ユークリッド距離
2. 市街距離：2点間の差の絶対値の総和
3. ミンコフスキー距離：上の2つを含む一般的測度
4. 重み付きユークリッド距離：単位系が異なる場合に行う標準化
5. マハラノビス距離：非類似性による指標

類似性の測度
1. ピアソンの積率相関係数：－１≦R(a,b)≦１のいわゆる相関係数
2. パターン類似率（Pattern Similarity）：積和を2乗和の平方根で除して標準化した0≦S(a,b)≦１の指数
3. 偏差パターン類似率：-1≦S(a,b)≦１の指数

質的変数
1. 一致係数
2. 類似比
3. 点相関係数

代表的なクラスター計算法
1. 階層的方法
　1. 最近隣法（鎖効果という問題が生じる場合がある）
　2. 最遠隣法（完全連結法ともいう）
　3. 重心法（セントロイド法ともいう）
　4. メディアン法
　5. 群平均法
　6. ウォード法（Ward's method）

2. 非階層的方法
　1. 最適化法：あらかじめ設定された基準を最適化するように分割を行う。
　2. 密度探索法

次のデータを例に考えてみる。ＡからＨまでの８個のデータとｘ、ｙの2変数。
x y
A 4 1
B 2 4
C 5 7
D 5 2
E 3 4
F 6 5
G 2 6
H 7 2

クラスター分析は個体間の距離を計測し、定義することから始める。
ここでは、最も簡単なユークリッド距離による計測を行う。

１　→　２　→　３　→　４

********　step1：Rでやってみよう　*********************
dat01<-read.table("c:/00dat/6-18.txt",T)
dd<-dist(dat01)
ddhc1<-hclust(dd)

ddhc1<-hclust(dd,"single")
ddhc2<-hclust(dd,"complete")
ddhc3<-hclust(dd,"average")
ddhc4<-hclust(dd,"centroid")
ddhc5<-hclust(dd,"median")
ddhc6<-hclust(dd,"ward")

********　step２：Rで描画　*********************
par(mfrow=c(3,2))
plot(ddhc1,main="最近隣法")
plot(ddhc2,main="最遠隣法")
plot(ddhc3,main="群平均法")
plot(ddhc4,main="重心法")
plot(ddhc5,main="メディアン法")
plot(ddhc6,main="ウォード法")

********　step３：Rで描画その２　*********************
par(mfrow=c(2,3))
plot(ddhc1,hang=-1,main="最近隣法")
plot(ddhc2,hang=-1,main="最遠隣法")
plot(ddhc3,hang=-1,main="群平均法")
plot(ddhc4,hang=-1,main="重心法")
plot(ddhc5,hang=-1,main="メディアン法")
plot(ddhc6,hang=-1,main="ウォード法")

***************************************************
前回の課題データ
***************************************************

example2
（山際、田中、『心理データの多変量解析法』、教育出版、1997）

Kは「京都」で他は「小京都」と呼ばれる日本各地の市である。これを
x1:歴史の古さ
x2:寺社の多さ
x3:自然の豊さ
の10点満点で評価したのが次のデータである。

　 x1 x2 x3
K 8 9 8
B 3 5 10
C 2 3 12
D 4 7 15
E 6 1 10

主成分分析の解析手順は事例をこなすことで習得したほうがよい。
習うより慣れろです。

主成分分析の解説と例題
主成分分析の分析例

一般的な、統計解析的な手順としては
１．基本等計量
２．相関行列、分散共分散行列
３．固有値（寄与率）
４．固有ベクトル＝ウェイト
５．主成分得点
６．出力結果の整形
　　R出力をＥｘｃｅｌ等で編集して、自分なりに理解しやすい形に編集（整形）する。


Rにおけるデータファイルの入出力

これまでの例は比較的小規模なデータなので直接ベクトル形式でRコンソールから入力したが、多変量だけに大量のデータを扱うとなると、このやり方では厳しい。

ということでデータのファイル入出力関数を一つ覚えておく。
なお、RはExcelやAccessとのデータのやりとりも可能であるが、SASやSPSS、TSPといった他のソフトとのデータのやりとりを考えるとASCII形式のテキストファイルという汎用性の高いフォーマットの利用を強く勧めます。世の中、何があるかわかりませんからね。

次のファイルを指定された場所に保存してください。

課題データ

方法はいくつかありますが、手っ取り早く、ファイルをRで読み込むには
read.table（）関数を使います。

read.table（”ファイル名”）と指定します。
例えば【Cドライブ】の【00dat】というディレクトリに【test_01.txt】というファイルがあるなら
t01<-read.table("c:/00dat/test_01.txt")
とします。

ここでｔ01の中身を確認します。7行4列のデータです。
　 V1 　V2　 V3 　V4
1 　x1 　x2 　x3 　　x4
2　 1 　 2　 　3 　　 4　
　　　　～～～～～

1行目のV1云々は変数名（列タイトル）になります。
このファイルの1行目には既に変数名があるので、その旨、宣言します。
t01<-read.table("c:/00dat/test_01.txt",header=T)

このデータにはｘ１からｘ４まで4つの変数がありますが、【t01$x1】として呼び出すのは面倒です。
そこで
attach(t01)
とすると、『データフレーム』というRでの分析用データセットに変換されます。
こうすると【x1】とするだけで、その変数の内容が確認できます。

ではこのサンプルで主成分分析を試みます。
まず
summary(t01)
pairs(t01)
cor(t01)
でデータ構造を確認します。
　→　このデータ群にはどのような特徴がありますか

主成分分析に進みます。
pca<-princomp(t01)
summary(pca)
【Proportion of Variance：寄与率】に注目します。【Comp.1：第1主成分】にはどれだけの情報が集約されていますか。【Comp.２：第２主成分】はどうでしょうか。

主成分の意味を解釈し、主成分得点を求めます。
loadings(pca)
pcsc<-pca$score
第1主成分は、元のデータx1、x2、x3、x4とどのような関係にあるでしょうか。
同様に第2主成分はどうでしょうか。

par(mfrow=c(2,2))
plot(pcsc[,1],t01[,1])
このように散布図を出力して、x1からx4までのもとの変数と第1主成分得点との関係を見てみましょう。
par(mfrow=c(2,2))はプロット部を4つの領域に分割します。

計算結果は頑健ですが、解釈は自由です。この点が好みが分かれるところです。

次のステップです。
とりあえず、次のR関数を実行してみてください。
pcadist<-dist(pcsc,method="euclid")
pcaclust<-hclust(pcadist,metho="average")
plot(pcaclust,hang=-1)

これは主成分得点から【距離行列】を作成し、【クラスター分析】を実行するものです。
参考までに以下のR関数は主成分分析以前の元のデータに対するものです。
dt01<-dist(t01,method="euclid")
clust<-hclust(dt01,metho="average")
par(mfrow=c(1,1))
plot(clust,hang=-1)

クラスター分析とはどういうものだろうか？
詳しい説明は次回になります。

以下の課題データを主成分分析にかけ、
主成分得点をクラスター分析し、デンドログラムを各自のブログにUPしてください。

課題データ

> pca<-princomp(osen)
> summary(pca)
Importance of components:
Comp.1 Comp.2
Standard deviation 2.5211880 0.3082206
Proportion of Variance 0.9852745 0.0147255
Cumulative Proportion 0.9852745 1.0000000


参考までに以下に記述しておきます。
> do<-c(7.2,9.4,5.2,3.8,8.1,8.6)
> bod<-c(1.3,0.8,3.9,5.0,1.5,0.9)
> osen<-data.frame(do,bod)
> osen
do bod
1 7.2 1.3
2 9.4 0.8
3 5.2 3.9
4 3.8 5.0
5 8.1 1.5
6 8.6 0.9
> pca<-princomp(osen)
> summary(pca)
Importance of components:
Comp.1 Comp.2
Standard deviation 2.5211880 0.3082206
Proportion of Variance 0.9852745 0.0147255
Cumulative Proportion 0.9852745 1.0000000
> plot(pca)
> plot(pca$scores)

> loadings(pca)

Loadings:
Comp.1 Comp.2
do 0.773 0.634
bod -0.634 0.773

Comp.1 Comp.2
SS loadings 1.0 1.0
Proportion Var 0.5 0.5
Cumulative Var 0.5 1.0
> pca$scores
Comp.1 Comp.2
1 0.7077761 -0.62662916
2 2.7260399 0.38164218
3 -2.4873407 0.11581851
4 -4.2674045 0.07876326
5 1.2769263 0.09867632
6 2.0440029 -0.04827111
>

前回の例題データのスペルが間違っていました。
正：waist　　　　誤：west

前回やったこと
Rによる回帰分析
複数の変量があるときの回帰分析を試しました。
2変数以上の場合は変量間の関連性を如何に読み取るかが重要で、マトリックスプロットによる視覚的把握をRで行いました。

今回のマスターしてもらいたい分析手法
　　あるいは身につけてほしい分析道具

主成分分析

多変量解析といえば、まず最初に主成分分析がくることが多い。
最も基本的な手法といえる。

どのように使うかを、Rのサンプルデータを使って試してみる。

統計学のテキスト等には歴史的エポックとなった有名な実験データが引用されることがある。大抵の場合、かなりな量であることが多いが、Rにはそのようのデータが既にデータセットとして準備されている。

Irisというデータは中でも群を抜いて有名なものではないだろうか。いわゆるアヤメのことであるが、その属の中の３種50標本のがく片の長さと幅、花弁の長さと幅の4変数の測定値である。Rには植物学者Edgar Anderson's Iris Dataとして収録されている。大元はR.A.Fisherの1936年の論文のデータである。なのでR登場以前はFisher's iris dataと称していた。

Rに付属しているデータはdata()関数で呼び出す。data(iris)とすれば特定のデータを呼び出すことができる。なお、sepalががく片、petalが花弁である。

とりあえずデフォルト設定でのRのサンプルデータは以下の関数で調べることができる。
data()

色々ありますが、CO２濃度や太陽黒点など、よく見かけるデータもあります。



irisのデータは次のように指定すると使用可能になる。
data(iris)

とりあえずマトリックスプロットしてみる。
pairs(iris)



多変量プロット（マトリックスプロット）が出力されるが、Listの5列目は文字データなので5列目を除いて指定する。配列は次のように指定する。

pairs(iris[1:4])



因みに、
pairs(iris[1:4], pch = 21, bg = c("red", "green3", "blue")[unclass(iris$Species)])
これはpchがプロットされる記号（symbol）の指定で、bgは色の指定です。

iris$Speciesのようにオブジェクト内の要素は＄でつなげて指定する。Speciesは3種のアヤメの名前があるので一つ目が赤、２つ目が緑、3つ目が青を指定している。

5列目を削除して新たに『 iris.x 』というデータを定義する。-5がその指定である。
iris.x<-iris[,-5]

以上で前準備終了。次が本題。

まず主成分分析の結果をpcaという名前に保存します。
pca<-princomp(iris.x)

結果は例によってsummaryで確認します。
summary(pca)

固有値というものです。
loadings(pca)

主成分得点の散布図です。pca結果内に得点がscoreとして出力されますので『＄』で【オブジェクト＄取り出す変数】という書式で取り出します。
plot(pca$scores)
plot(pca)

主成分得点をpcscというデータセットにします。
pcsc<-pca$score

以下、つらつら出力してみます。
plot(pcsc[,1])
plot(pcsc[,2])
plot(pcsc[,1],pcsc[,2])
plot(pcsc[,1],pcsc[,3])
plot(pcsc[,2],pcsc[,3])
plot(pcsc[,1],iris[,1])

主成分得点のマトリックスプロットです。さて元データのマトリックスプロットとどう変わったでしょうか？
pairs(pca$scores)

次はバイプロットと呼ばれるメソッドで、行列を逆転させた主成分分析と思ってください。説明は後述。
要は第1主成分と第2主成分の部分空間（データに対する反応の構造）の散布図です。
biplot(pca)

なお、以下の関数で表計算ソフトようなworksheetのように扱えます。
edit(pca)

さて、よく分からないままつらつらと主成分分析の流れを見てきましたが、以下で詳しく説明します。

チェックすべきKey Wordは
・固有値　　→　因子負荷量　→　寄与率　
・固有ベクトル　　→　　主成分得点

　　そしてデータ空間の頑健な構造と自由な解釈（主観的という人もいる）

主成分分析に関する解説


課題

前置き

琉大では３年毎に見直される情報システムだが、今年度がその年に当たってしまった。システムの改善は望ましいが、統計処理システムがSASからRに変わった。それはそれで好ましいが、Rはfreeなのだから各自でインストール可能だし、むしろSを導入してもらいたかったところだ。ただこれまでのMapleとMatlabにMathematicaが追加されたのは素晴らしい。一応、数式処理ソフトは定番が揃ったことになる。
何とかならんものかと情報センターに問い合わせると、SASは医学部の実習室でないと使えないと、あっさり断られた。医療や薬学、保健分野でのSASの実績は大きいが、最近は保険、金融でもB=Sモデルやオプション、金融商品の設計のために基幹システムとして導入されているケースも多い。またGISや最適化問題でも多くの資産が蓄積されている。琉大では農学の新城先生はテキストの発行など第１人者でもある。そのSASが今年から、実習では使えないというのは非常に残念。とはいえ直接センターに行けばCDを借りることができます。興味とやる気のある方はチャレンジしてみてください。

先週やったこと。
対話型でRを使用したが、直接、複数行を入力したり、ファイル入力もできる。
以下は先週実行したコードである。
uri=c(8,9,10,12,11,13)
kou=c(5,5,7,5,8,12)
sal=c(6,8,10,12,12,12)
est1<-lm(uri~kou)
est2<-lm(uri~sal)
summary(est1)
summary(est2)
plot(kou,uri)
lines(kou,fitted(est1))

uri(売上),kou(広告費),sal(セールスマン数)の３変数を定義し、単回帰とグラフのプロットを試した。

今回やること
単回帰は説明変数が一変数だが、重回帰は２変数以上になる。

単回帰：ｙ＝a+ｂ・ｘ
重回帰：ｙ＝a+ｂ・ｘ+ｃ・ｚ+・・・

直感的な違いは散布図での表示が複雑になることだろうか。

ようは説明変数がたくさんあるということ。

先週使用したデータで重回帰をやってみる。
売上＝ｆ（広告費、サラリーマン数）
式：uri=定数項+係数１×広告費+係数２×セールスマン数

推計する前に変数の関係を確認してみる。
・相関行列

まずデータセットを作成する。３変数を一組として扱う。これは変数やデータ数が多くなると必須となる。

支店別データなので、データセット名をsitenとしてみる。

siten<-data.frame(uri,kou,sal)
cor(siten)

これで相関行列が出力される。桁数を指定するときはround関数を用いる。
round(cor(siten),4)
数値ではイメージしにくいのでマトリックスプロットで見る。
pairs(siten)

pairs関数がマトリックスプロット用の関数で、この他にも様々なオプションがある。

重回帰は次のように指定する。
sitenlm<-lm(uri~.,data=siten)
summary(sitenlm)

見方は、変数が１個増えた以外、単回帰と同じである。

手順のまとめ：
１．データセットの定義
２．相関行列、マトリックスプロットで変数間の関係をチェック
３．重回帰式の推計

次のデータを用いて、上の手順を実行し、マトリックスプロットを出力して、各自のブログにupしてください。また、記事の中でsummaryで出力された内容について評価（コメント）してください。

weight<-c(50,60,65,65,70,75,80,85,90,95)
height<-c(165,170,172,175,170,172,183,187,180,185)
waist<-c(65,68,70,65,80,85,78,79,95,97)

このデータでbodyというデータセットを定義する。
被説明変数はweightにします。

++++++++++++++++++++++++++++++++++
++++++++++++++++++++++++++++++++++
応用編

回帰診断
結果の解釈について、このモデルが使えるか否か、を判断する材料を示す。
これは最近の回帰分析では流行の手法なので、簡単に触れておくが、詳細は後日、説明します。
方法は回帰結果をプロットするだけですが、４つのグラフが出力されるので、画面を４分割します。

画面の分割
par(mfrow=c(2,2))
結果の出力
plot(sitenlm)

統計解析と情報処理のトレーニング

これから行う作業は「入力→出力：input/output：Ｉ/Ｏ」の繰り返しとなります。

　入力　　　　　出力
・データ　→　計算結果
・読取　　→　記述
・校正　　→　Web出力
などなど　etc...

どのような情報を出力するかは、如何なる情報を入力するかに密接に関わる。
つまり分析の目的なり、テーマの設定なりが大切だと言うことです。



目的の設定やデータの収集のポリシーにしても、どのような解析手法のメニューがあるかにかかってきます。そこで今回は解析手法と解釈の方法について検討していきます。

解析方法のメニュー化されたマップ

※他にも多くの方法があるが、現在私が対応でき、Rで手法が提供されているものを中心に記述した。

この中で、手っ取り早く理解できるのが回帰分析と主成分分析です。
両者は入門編の横綱格に相当するといっても過言ではない。

回帰分析のイメージ

この図はYとXのデータの関係を
　　Y＝a+ｂX
という式で近似したものと考えて良い。
Yを目的変数（従属変数）、Xを予測変数（独立変数）といい、
aが定数（切片）、ｂが回帰係数であり、この式を回帰式という。

次のようなデータがある。
　　Y　　X
1　3　　2
2　2　　2
3　4　　3
4　4　　4
5　5　　5

このデータをプロットし、上の回帰式を求めてみよう。

１．Rのeditorからデータを入力する。
２．グラフ出力＝plotする。
３．回帰モデルの設定
４．出力を見る

参考

続きを読む

bloｇ開設した方は、ここに登録されているか確認してください。

学籍番号とリンク先が対応しているか確認してください。間違っていたら申し出てくさい。修正します。

～～～～～～～～～～～～～～～～～～～～～～
～～～～～～～～～～～～～～～～～～～～～～
Rを使ってみよう。

RWiki
・RWikiはRubyで開発されたWikiで、Rの日本語に関する情報のほとんどが網羅されている。
・Rの日本語文献は最近数多く出版されているが、
The　R　Book（WebCatPlus）
がおすすめ。琉大図書館にはないが、沖国、沖大、沖縄高専にはあるようだ。不思議。
他の参考文献に関してはRWikiを参考にしてください。

ところでSASにしろSPSSにしろ、Sも目の前のマシンにインストールしなければならない。Rもしかり。とことろがRには"R on Web"というサイトがあり、ある程度のことは体験することができる。
そこで、Rをインストールする前にブラウザさえあれば、どこででも実行できる"R on Web"を使ってみることにします。


R　on　Web

上記リンクを開いてください。こんなかんじになっていると思います。


この部分をマウスで範囲選択してコピーします。


今度はコードを記述するボックス部分に貼り付けて、ボックス下の「Submit」ボタンを押してください。


しばらくすると計算結果が出力されます。


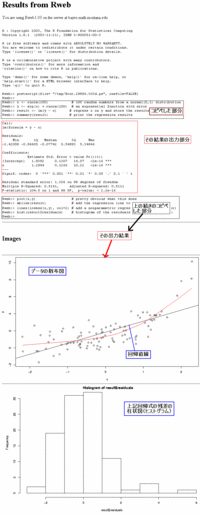
コードの説明

x ＜- rnorm(100)
・ｒnormは正規乱数を発生させる関数で、ここでは100個の正規乱数を発生させ、ｘという変数に代入しています。
・代入は「＝」ではなく「＜－」で記述します。

y ＜- exp(x) + rnorm(100)
・ｘを指数変換し、それに100個の正規乱数を加える。こうしてできた系列をｙという変数に代入。

result ＜- lm(y ~ x)
・lmは線形回帰の関数で「ｙ＝a+ｂ・ｘ」という式を当てはめ、aとｂを推計する。推計結果をｒｅｓｕｌｔという変数の代入。
・このように推計式の場合、Rは「＝」でなく「～」とイコールでなく、チルダを用いる。

summary(result)
・summaryはその名の通り、結果を要約して出力する。回帰結果が保持されているresultの内容を表示する。

plot(x,y)
・ｘとｙをプロット（散布図）する。

abline(result)
・resultの中にある回帰係数aとｂを使った回帰線を描き、プロットグラフに追加する。

lines(lowess(x,y), col=2)
・Rには多くの平滑化関数があるが、その中の一つで、colは色を指定し、結果をlineで描画している。

hist(result$residuals)
・histはその名の通りヒストグラムを描画する関数で、回帰計算の結果が保持されているresultから残差系列を抜き出して、描画している。
・residualsはｌｍ関数の結果として出力される数値系列で、その名の通り残差系列である。
Rの書式では、ある処理を施したあと、その結果として出力される数値等に対して、「キャラクターダラー＄その変数名：ここではresult$residuals」というように指定することで結果の一部を取り出す。

何を今更、と思うかもしれませんが、ワープロと表計算の利用方法として、Web上で表示する各種チャートやグラフを作成する、というのが今回の趣旨です。

例えば、以下の書き込みのようチャートやグラフはどのようにして作成し、Web上にUPするのか？

・figure1


・figure2


図をクリックすると、それぞれサンプルのワードとエクセルが起動します。

本日の教材はこちらです。


ti-da.blogへの登録＝＝＞こんな感じだ！

過去ログ等へのリンク

トップページ

リンクページ

リンクページ

E-decomp
http://tswww.ism.ac.jp/kawasaki/memo.htm